Like anything else in the universe, we would like to know how galaxies got that way. There are starting to be observational limits on the redshift of galaxy formation from both directions - stellar evolution and homogeneity of the microwave background. Note again that an observer's and theorist's times of galaxy formation may differ. As Peebles (1989, in The Epoch of Galaxy Formation, Kluwer, p. 1) remarks, an observer would likely date galaxy formation when most of a galaxy's stars are born, while a theorist would time the process from the collapse of a substantial portion of a galaxy's present-day mass out of the Hubble flow. Thus a galaxy might be young in stellar terms but dynamically well-evolved. As just discussed under galaxy evolution, there are several galactic chronometers that may run at different rates for various kinds of galaxy. The main things we need to account for are the ages of galaxies, their masses, and the distinction between bulges and disks.
In a sense, galaxy formation is like star formation (which we don't understand either) on a larger scale, with the added complication of a superimposed Hubble flow. Given the existence of a density enhancement (we'll come back to this), a mass will collapse if it exceeds the equivalent of the Jeans mass. In fact, as Zel'dovich and Novikov show (Relativistic Astrophysics, vol. 2, U. Chicago, p. 244), the Jeans theory is a remarkably good approximation of the relativistic result. In this case, a perturbation will lead to collapse if it has wavelength sufficiently large: Λ > Λ J = 27 (T/μ )1/2 ρ0 1/2 parsecs, and consequently mass greater than the Jeans mass M > MJ = 33 (T/ μ3/2 ρ 0-1/2 in solar masses. In these expressions, μ is the mean molecular weight (1 for neutral hydrogen, 1/2 for ionized hydrogen, and so on), the temperature is in K, and ρ0 is the unperturbed density in units of 10-24 g/cm³. In more useful units, Longair gives the conversion MJ = 3.75 × 1018 / Ω Bh²) in solar masses, for the case dominated by ordinary matter.
In dealing with density perturbations, it is usual to do the equivalent of Fourier decomposition and treat the evolution of various wavenumbers (frequency or wavelength). Many workers start with a Kolmogorov spectrum, in which the energy density on a scale R goes as R1/3. Physically, this arises through turbulent viscosity damping different scales at different rates. One could, of course, obtain interestingly different results if there are mechanisms that can pump energy on specific scales.
So where did these perturbations come from? Statistical fluctuations in particle density within a uniform field won't do it. There are of order 1068 nucleons in a galaxy (neglecting dark matter, whose effects only make matters worse). This gives relative density fluctuations ΔN/N ~ 10-34, much too small for the most nonlinear growth to give galaxies by z=5. The relative fluctuations are smaller for more efficient galaxy formation. Dicke and Peebles (secondhand reference) postulated that perturbations around the Jeans mass quickly make objects like globular clusters, and that it is the statistical fluctuations of this sparse population (more like 10-3) which seed galaxy formation - an interesting idea with only two miracles required. Note that temperature or velocity perturbations could have been present, and effective in triggering collapse, as well as ordinary density fluctuations. We might try considering primordial fluctuations (pushing our ignorance back as far as possible), but there is no signature of these in the microwave background. However, this still allows primordial fluctuations carried by nonbaryonic matter, which need not be coupled tightly to the thermal radiation field before recombination.
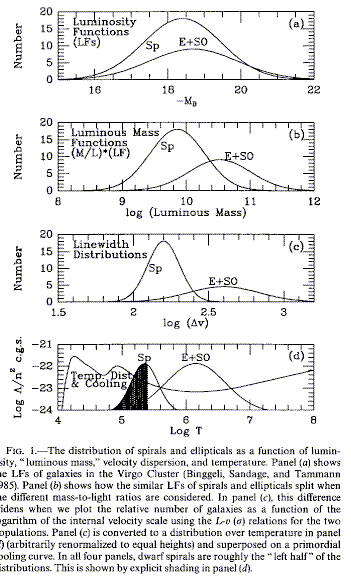
The history of the collapse, as in star formation, will be greatly influenced by cooling of the material; strong radiative cooling will hasten the collapse and give a more compact final configuration. Recall here the peculiar behavior of hot gas in cooling flows as an example. For example, Lake 1990 (ApJLett 364, L1) considers different kinds of galaxies (dwarfs, spirals, ellipticals) to result from different ratios of dynamical, cooling, and Hubble times, together with whether cooling at the relevant densities does or does not become more efficient at lower temperature. His Fig. 1d (shown by permission of the AAS) superimposed a cooling curve on the approximate temperature distributions of spirals and ellipticals, showing that this is at least plausible if we take a characteristic temperature from present-epoch global dynamics:

Assorted applications of the gas cooling function can be found throughout studies of galaxy formation. Peacock points to Blumenthal et al. 1984 (Nature 311, 517), who point out that galaxies and clusters collect in diferent parts of the (density, temperature) plane, such that dissipation is indicated for galaxy formation (i.e. there has been time for galaxy-sized gas masses to cool but not cluster-sized masses).
Star formation may have been active during the collapse. This further complicates tracing the evolution of a protogalaxy, since stars and gas are dynamically very different. Also, the first generation of stars may have driven vast outflows of material as they heated their surroundings, blew winds, and exploded as supernovae (producing some of the gas now seen in clusters). The low metallicity and high background temperature (recall that would be 2.7 K × (1+z)) complicate our understanding of the appearance of the original ("population III") stars. For at least the gas, the course of the collapse would not be adiabatic, isothermal, or even mass-conserving.
At least for disks, we strive to understand where their angular momentum came from. Pure collapse would introduce none, and it's hard to see where vorticity would arise in the early universe without invoking ad hoc behavior of the density fluctuations. A popular suspect has been tidal torquing, in which the protogalaxy is nonspherical and its closest neighbors exert a tidal stress that imparts net angular momentum. This works because the companions are on average receding, so the galaxy is left with a spin fossilizing the initial conditions and not averegaed to zero by later evolution. One might seek correlations produced by this process in isolated bound binary systems; no detections have been reported. The expected specific angular momentum depends on the characteristic companion distance and the shape of the protogalaxy at the time when single companions were most efficient at tidal torquing. Spin could also be produced in mini-mergers, as fragments of sub-galactic mass come together. In this case, spin arises from off-center impacts (as discussed in the outer solar system). Chernin has studied the appearance of vorticity by propogation of shock fronts across density gradients.
We end up with one major problem: how could galaxies form so fast from the homogeneous background seen in the 2.7 K radiation? COBE and its successors give values of order 3 × 10-5 for temperature fluctuations on scales of several degrees. Following Zel'dovich and Novikov (p. 445), the angular scale of a fluctuation of mass M at contrast temperature 10-3 would be θ = 10 arcminutes × Ω2/3 (M/1014 solar masses), setting the most appropriate angular scale. Silk (1968 ApJ 151, 459) gave the relation, also seen in the previous lecture, ΔT/T = Δ ρ / 3 ρ. There are unknowns in going from such small perturbations at z ~ 1400 to whole galaxies by about z=7.
A crucial role was played by whatever the dark matter is. Longair devotes an entire chapter to setting out the "classical" scheme for galaxy formation in a purely baryonic Universe, solely to illustrate that it doesn't work. It is the perturbation spectrum of this dominant mass component that matters for galaxy formation. The effects on galaxy formation differ depending on whether the dark matter is hot, warm, or cold. These refer to its velocity dispersion relative to the normal matter. For example, neutrinos of low mass would be hot dark matter, with large individual velocities. Hot dark matter makes galaxy formation very difficult - density enhancements are smeared away by rapid particle motions before they can collapse. The only unstable masses are far too large (remember MJ ~ T3/2 above). Cold dark matter is more popular, since this stuff is gravitationally bound and can fall into perturbations just as well as ordinary matter. However, it undergoes a fully dissipationless collapse. A problem here is that any dark matter cold enough to allow galaxy-size masses to form also predicts an uncomfortable amount of delayed galaxy formation. This gives difficulties with limits on baryonic IGM. There is not a clear piece of parameter space that simultaneously satisfies the IGM and microwave-background limits while still producing things of galactic mass. Plainly there is something important we don't know about galaxy formation.
There are several "guerilla" pictures for galaxy formation. Unfortunately, none is well developed or specific enough to be testable. A plasma-based picture has been pushed recently by several plasma theorists, but this seems to require special initial conditions and a special epoch at which we live. To be fair, astrophysicists are being dragged into the realization that magnetic fields and plasma processes are important on large scales. Then there is a scheme for building galaxies out of their nuclei, postulated for example by Ambartsumian. Again, there is so little overlap with familiar physical processes that it is not clear what we would expect to see in this picture.
There are big plans to push relevant observations in the coming decade. Key questions are:
The lack of a Gunn-Peterson trough in the spectra of quasars long ago established that the intergalactic medium must be highly ionized. Since we see radiation from the initial recombination as the cosmic microwave background, it must have been reionized sometime later. This reionization epoch is important for the history of galaxy assembly and our ability to observe high-redshift objects; its progress likewise carries clues to the early history of galaxies and QSOs.
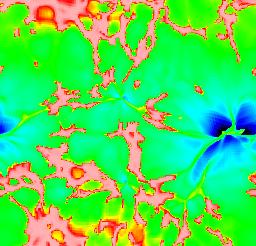
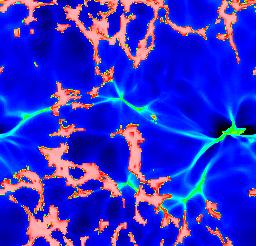
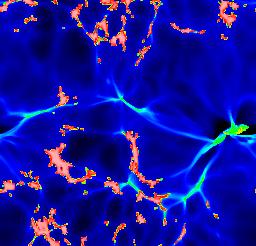
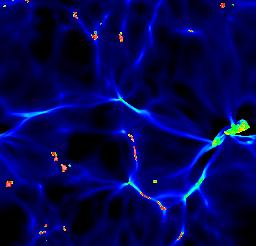
Numerical modelling of the recombination era tracks the same features seen in modelling H II regions - expanding ionization fronts, surrounding partially ionized zones - now set against the backdrop of cosmic expansion. The results have been reviewed in detail by Loeb & Barkana (2001 ARA&A 39, 19). As the ionized volumes ("Strömgren spheres") expand around individual ionizing sources, it is useful to follow Gnedin (2000 ApJ 535, 530) in distinguishing phases before, during, and after the overlap of these volumes. Initially, each ionized bubble expands independently, fully surrounded by neutral material. The rate of expansion depends on the ionizing luminosity, shape of the ionizing spectrum, and density distribution of the neutral gas. The ionizing sources are likely to be in the highest-density regions, being surrounded by gas which recombines fastest. The ionization structure will trace in reverse the gas density in the "cosmic web", with denser filaments becoming ionized later as the flux finally overcomes their (falling) recombination rate. Late in recombination, this has the somewhat paradoxical result the regions of neutral gas will still exist quite close to the ionizing sources while much more distant low-density regions are fully ionizing and remain so. The following images trace the development of ionized fraction, taken from Gnedin's WWW site.
 |
 |
 |
 |
 |
 |
 |
 |
Hydrogen naturally dominates the physical state during recombination. Helium still plays a role, since the ionization potential for He II is 54 eV, making its appearance a still later event. In low-density regions, reionization of He II took place near z=2.7 (Kriss et al. 2001 Science 293, 1112).
On the observational side, there are a series of effects to show that we are seeing into and before the epoch of reionization. First we expect the classic signature of a neutral intergalactic medium, Gunn-Peterson absorption . At low redshifts, this takes the form of the Lyman α forest, discrete absorption features from the densest regions of the IGM, where the neutral fraction is highest (although in absolute terms still quite small). The density of features in the Lyman α forest increases with redshift, both as a result of genuine evolution in the density (and thus recombination rate) of the gas, and from cosmology, due to the nonlinear mapping between redshift and distance along the incoming ray. The appearance of genuinely diffuse, space-filling neutral gas will then be as excess absorption beyond the extrapolated behavior of the narrow individual lines, or, at high enough spectral resolution, a complete "trough" of absorption beyond what one would expect from the total of individual lines. This has been observed for QSOs at z >6, found from the Sloan Digital Sky Survey (SDSS) as reported by Becker et al. (2001 AJ 122, 2850). The rapid increase in H I opacity across the range z=5.7-6.4 is strong evidence that we are seeing the end of reionization at these redshifts. These Gunn-Peterson troughs imply only the end of reionization. A neutral-hydrogen density of only a small fraction of the overall baryon density will produce stronger absorption than we can reliably measure, since all optical depths τ > 5 are observationally indistinguishable. A fully neutral IGM should produce τ > 100, so other signatures are needed to measure its neutral density. As pointed out by Miralda-Escude (1998 ApJ 501, 15), at such high column densities, the damping wings on the Lyman α absorption line become very strong and broad, so that the absorption signature is a broad absorption edge of predicted shape, starting ~100 A redward of the QSO's Lyman α wavelength. Finally, scattering of microwave-background photons by ionized material will imprint a signature of reionization on the polarization structure of fluctuations in the microwave background as detected by the Wilkinson Microwave Anisotropy Probe (WMAP) suggesting reionization at z=11-30 (Bennett et al. 2003, astro-ph/0302207).
Once a significant volume of the ISM has become ionized, we expect ionized (and thus transparent) volumes around indivual radiation sources. These would appear as holes in the absorption when a line of sight passes through such a volume, in a more powerful version of the proximity effect. This effect appears as a decrease in the number of Lyman α forest features near the redshifts of QSOs, whether the background QSO whose spectrum is being measured or fortuitously located foreground objects within a Mpc or so of the line of sight. As long as the differential Hubble expansion across an ionized volume is greater than the span of absorption wings from adjacent material, an ionized region will appear as a local deficit in absorption (as depicted by Loeb & Barkana 2001).
An emission signature of the final stages of reionization is expected, which could help specify its redshift. Broad and asymmetric Lyman α emission is predicted from blank sky areas in all directions (Baltz et al. 1998 ApJL 493, L1), whose intensity depends largely on baryon density, with a wavelength determined by the recombination redshift. A sensitive search for this feature has used a large number of HST STIS spectra covering blank-sky regions (Windhorst et al. 2001, in Deep Fields), yielding to date an intensity limit for this feature anywhere in the redshift range z=6-9 somewhat higher than typical predictions.
Emission features may also be observable from the expanding H II regions around individual sources earlier in reionization. While the optical depth in the Lyman α transition will be enormous, some photons can be scattered far enough to the red wing of the line to escape. The situation is analogous to escape of Lyman α from a galactic wind, with the Hubble expansion playing the role of the wind's velocity field. Only the red wing matters, since photons scattered to the blue wing are promptly absorbed by foreground gas at a redshift for which the photons are close to the line center. Loeb & Rybicki (1999 ApJ 524, 527) have shown that we may hope to detect the halos of scattered light around very luminous objects at z~10, particularly with JWST. We might be able to see the H II regions themselves around some objects in dense environments at smaller redshifts, if the falling neutral fraction does not outweight the much smaller absorption optical depth to Lyman α.
Since we now find quasars into the epoch of reionization, strong radio sources from active nuclei may exist at significantly higher redshift. In principle, ionization structure at such epochs may be traced by highly redshifted 21-cm absorption (Carilli, Gnedin, & Owen 2002 ApJ 577, 22). While probably an endeavor for the next generation of radio telescopes, this would offer unique probes of these early epochs free of losses due to dust and Lyman-continuum absorption.
Further pursuit of most of these signatures to redshifts much beyond z=7 requires achieving high sensitivity in the near-infrared bands, which faces formidable obstacles from the atmosphere's own molecular and thermal emission for ground-based instruments. Progress can be made in spectroscopy of compact objects using the new generation of 8-10m telescopes, particularly those optimised for infrared performance, and techniques to limit the impact of night-sky emission. These include spectrographs with airglow suppressors, which disperse the light spectrally and mask out wavelengths with strong OH airglow, and spectrographs with high dispersion so that these wavelengths can be ignored while retaining nearby wavelength bins with source information. For diffuse emission, such as scattered Lyman α halos around early QSOs or intense starbursts, the advantage of getting above the atmosphere is probably required.
A key question must be answered from observation - what was the source of reionizing photons? One could imagine that either stars or active nuclei could provide the energy. Current surveys suggest that QSOs fall well short of the space density required to be important, although they will certainly dominate in their immediate neighborhoods. From metallicity arguments, first-generation stars were not numerous enough to ionize more than their immediate cloud vicinities. Further into galaxy buildup, we can count bright galaxies at redshifts z~6 by Lyman-break selection, and find that there are too few luminous galaxies for their hot stellar populations to power reionization (Yan et al. 2003 ApJL 585, L93; Lehnert & Bremer 2003 astro-ph/0212431). This makes the most likely culprits lower-luminosity galaxies, which it is tempting to compare with the small, low-metallicity objects found in significant numbers at z=2-3 and sometimes termed "subgalactic". If most of the star formation at these epochs was in low-mass systems, there is a good fit to predictions from structure-formation simulations for a Universe whose matter density is dominated by cold dark matter (CDM), which gives bottom-up or hierarchical histories for mass clumping and hence galaxy building.
Because of the Hubble expansion, it requires vastly less ionizing radiation to maintain the ionization of the intergalactic medium than to ionize it in the early Universe. As a two-body process, the timescale for recombination varies as the product of densities np ne, which is to say np2 for fully ionized hydrogen. Ignoring for the moment the dependence of cross-section on electron temperature, the basic redshift behavior for the recombination timescale will be (1+z)-6 simply from density considerations. This has increased by more than 105 since the end of recombination for gas outside galaxies, at z~6.4.
The mean ionizing intensity from star-forming galaxies and AGN is ample to maintain an ionized intergalactic medium today. In fact, there may be evidence that the intensity of this intergalactic ionizing radiation sets the cutoff in column density for H I envelopes of galaxies (Maloney 1993 ApJ 414, 41). The ionization balance in low-redshift QSO absorption-line systems suggests that the harder spectra of AGN are most important in the present ionizing intensity, in contrast to the situation at high redshifts, as shown by the recent analysis of Scott et al. (2002 ApJ 571, 665). They show that the density of ionizing radiation needed to match the extent of the "proximity effect" in QSO absorption spectra matches that estimated for the current QSO population, and that this quantity has been dropping rapidly with cosmic time, by a factor of nearly seven for redshifts z < 1 and z > 1.
Last changes: 11/2009 © 2000-9