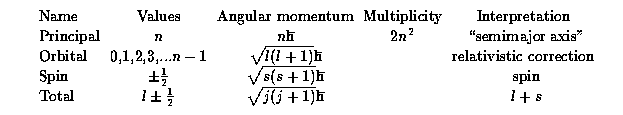
Because various emission lines sample different regimes of temperature, density, and ionization, emission spectra are uniquely powerful probes of conditions around active nuclei. Remember, though, that they do sample conditions around the central engine, which we can study only as it affects the surrounding gas.
Important references on emission-line processes are Osterbrock, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (University Science Books); Spitzer, Physical Processes in the Interstellar Medium (Wiley-Interscience); Aller, Physics of Thermal Gaseous Nebulae, and for specifics of AGN applications, Davidson and Netzer 1979 (Rev. Mod. Phys. 51, 715) and Peterson's AGN textbook.
Review of the recombination theory in the star-formation lecture will be helpful. Every state of an atom or ion has quantum numbers of importance here as follows:
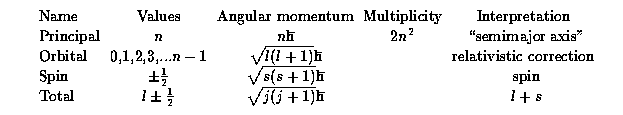
Each (l,s) pair has multiplicity g = 2s+1 - the number of energy levels with distinct j. For historical reasons, different values of l=0,1,2,3 are denoted in spectroscopic notation by S,P,D,F (strong, principal, diffuse, faint), then G,H,... A spectroscopic term (atomic state) is denoted by n gLJ.
For any possible transition between two states m,n there exist the Einstein transition coefficients Amn, Bmn, Bnm. These give the probabilities of transition between these two states. Amn is the spontaneous transition rate per unit time per atom, formally given by
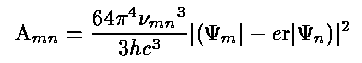
in the first-order (electric dipole) expansion. The B values - the stimulated emission coefficient and the absorption coefficient - are related as may be shown by considering thermodynamic equilibrium and detailed balance:
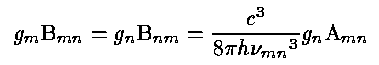
Here, for incident radiation intensity at the frequency νmn equal to Uν, the probability of an induced downward transition, or stimulated emission, is BmnUν. Transitions with Δl = ± 1 or Δs = ± 1 are dipole (permitted) transitions. Other kinds, via electric quadrupole or magnetic dipole moment, are possible but have generally much lower Amn; hence the term forbidden transitions. The upper levels in these cases are said to be metastable because of their relatively long lifetimes.
Application of these may be seen in a schematic few-level atom; these are all part of the "ground state" n=0. Only 4-5 of the possible transitions have high enough probabilities to be observed in a realistic case, satisfying the appropriate selection rules..
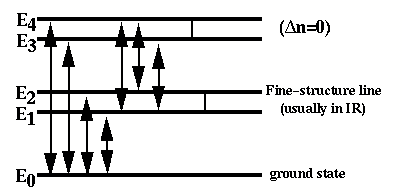
An electron may reach an upper level for any of a number of reasons:
Various of these are important for different ions. Having already discussed pure recombination, we still need to deal with collisional excitation of "forbidden" lines. These are important coolants in the energy balance of plasmas at T ~ 104 K because only the heavy elements have excited levels at the appropriate energies of a few eV. H and He don't.
Collisional excitation and forbidden-line emission. The collisional excitation cross-section for a transition from state 1 to 2 is given by
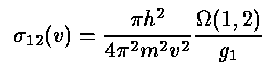
in which the electron's velocity and mass are used. The v2 factors out the strongest dependence explicitly to make the Ω term better behaved with electron energy, and easier to interpolate. The Ωs require direct quantum calculations; most astronomers take the easy way out and look them up. The rate of collisional excitations between states 1 and 2 per unit time and volume is
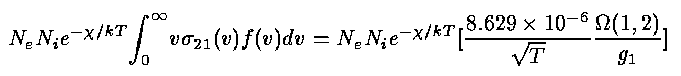
if Ω(E) is constant over the relevant range. As in the recombination case, a thermal (Maxwellian) distribution of electron velocity will generally be expected; significant deviations are possible if there are additional energy sources (beyond photoionization) for the electron population. The quantity in square brackets is often denoted by q12. There exists a relation between Ω for a single term and that for a set of closely spaced levels
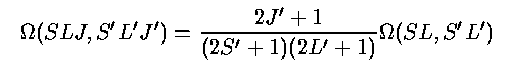
if S=0 or J=0. This means that certain line ratios are fixed by statistical weights in the atoms - the ratio of photon numbers in the lines is the ratio of statistical weights, and the ratio of line intensities is this value modified by the ratio of frequencies. This accounts for the (nearly) 3:1 ratios in line pairs such as [O III] λ4959,5007 Å, [N II] λ 6548,6583 Å, and [O I] &lambda 6300,6363 Å.
Critical densities. Decays from such collisionally-excited transitions are usually forbidden (except for some strong UV carbon and Mg lines). The cooling rate is then Lc = Ne Ni q12 h ν21 if the atoms remain in the excited state until they radiate. This is true as long as the density is much less than the critical density at which collisional de-excitation happens as often as radiation. This is a useful diagnostic - if we don't see certain lines of an ion, it may be because the density is too high for their radiation to occur. This happens when the mean time between collisions is comparable to or less than the radiative lifetime A21-1. The critical density for a given transition is, by definition, that for which these rates are equal; note that we need to include all collisions that will change the electron's state. Per unit volume, at the critical density Ncr,
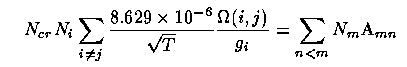
or using the q notation
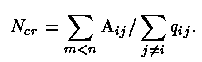
This may usually be calculated for a temperature 104 K (nebulae range from about 0.8 to 1.3 times this). Theoretical uncertainties lead to errors of order 25%.
Some useful values of the critical density are:
| Identification | Wavelength (Å) | log Ncr (cm-3) | Identification | Wavelength (Å) | log Ncr (cm-3) |
| [C III | 1909 | 9.0 | [Fe VII] | 5721.1 | 7.6 |
| [O II] | 3726.1 | 3.5 | [N II] | 5754.6 | 7.5 |
| [O II] | 3728.8 | 2.8 | [Fe VII] | 6086.9 | 7.6 |
| [Fe VII] | 3760.3 | 7.6 | [O I] | 6300.3 | 6.3 |
| [Ne III] | 3868.8 | 7.0 | [S III] | 6312.1 | 7.2 |
| [Ne III] | 3967.5 | 7.0 | [Fe X] | 6374.6 | 9.7 |
| [S II] | 4068.6 | 6.4 | [N II] | 6583.4 | 4.9 |
| [O III] | 4363.2 | 7.5 | [S II] | 6716.4 | 3.2 |
| [Ar IV] | 4711.3 | 4.4 | [S II] | 6730.8 | 3.6 |
| [Ar IV] | 4740.0 | 5.6 | [Ar III] | 7135.4 | 6.7 |
| [O III] | 5006.9 | 5.8 | [O II] | 7319.9 | 6.8 |
| [Fe VIII] | 5159.0 | 6.5 | [O II] | 7330.2 | 6.8 |
| [Fe VI] | 5176.4 | 7.6 | [N I] | 5197.9 | 3.3 |
This table is mostly taken from the values listed by Appenzeller and Östreicher 1988 (AJ 95, 45); additional ones are listed, for example, in Table 3.11 of Osterbrock. All lines produced by radiative decay from a common upper level have the same critical density. Density measurements are possible from lines of the same ion with different Ncr; the line ratio then depends on density if everything else is held constant. Species such as [O III] and especially [S II] have sets of lines that are more sensitive to density than temperature over useful ranges. Note the designation of the [C III semi-forbidden line.
There is a general relation between ionization potential χ of an ion and the critical densities of its forbidden transitions (just happens that way) which blurs the distinction between ionization and density gradients. The [O I] lines are important here as a neutral species with very high critical density.
Temperature and Density Determinations: All line ratios that are not fixed by atomic parameters are to some extent dependent on both temperature and electron density. However, for certain ratios the dependence on one is much stronger, and these are particularly valuable as diagnostics of physical conditions in nebulae.
For temperature determinations, we want to measure the ratio of electrons with different energies - so we look for pairs of lines of the same species with very different excitation energies. The most-used example is [O III] with lines at 4363 and 4959+5007 Å. As long as the density is below the critical density for the intermediate level from which the two strong lines arise, the populations of all the levels involved reflect the electron energy distribution and thus the electron temperature. As an analytic approximation,
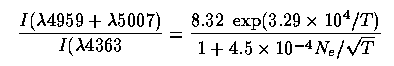
The line ratio is about 1000 at 6000 K, dropping to 100 at 14000 K. However, beware that a one-zone model is seldom appropriate; a small amount of hot gas may skew the results. Also, high-density gas will show relatively strong λ 4363 because the other lines are collisionally de-excited. There is a similar set of lines for the next ion down in the same isoelectronic sequence, [N II] with lines at 5755, 6548, and 6584 Å.
For densities, we want pairs of lines from energy levels with nearly the same excitation energy but quite different A-values; now the thermal populations will be the same to within the statistical weights, and the line intensities will tell what fraction of atoms in each level are collisionally de-excited before radiating. The premier examples are [S II] λ 6717,6731 and [O II] λ 3726,3729. Cruder determinations are possible using the fact that lines with critical densities far below the actual density will be invisibly weak - this is how densities in broad-line regions are determined.
Reddening may be determined by finding pairs of lines which are far apart in wavelength but have line ratios fixed by atomic physics. The best-known set is the ratio of [S II] lines in a quartet at λ 10287-10370 to a pair at λ 4069,4076, discussed by Miller 1968 (ApJLett 154, L57) and Allen 1979 (MNRAS 186, 1P). More (weaker) lines that may be so used are listed by Draine and Bahcall 1981 (ApJ 250, 579). Hydrogen or helium recombination lines are also frequently used to measure reddening; if the temperature is known (and a one-zone model is not too bad) they may be measured over an enormous wavelength range, but are frequently dominated by the tiny BLR or have highly velocity-composite profiles.
Ionization parameter. The ionization balance of a species emitting collisionally-excited lines is set by the local ionizing-radiation field (since the electrons are freed by recombination). However, the intensity of the lines (below Ncr is set by Ne, abundance of the emitting species and the electron temperature. Over a wide range of low densities, the ionization levels, and thus line ratios and appearance of the forbidden-line spectrum, are set primarily by the ratio (strength of ionizing radiation : Ne). This ratio is expressed as the ionization parameter in various ways. One useful dimensionless form is the ratio of ionizing photon and particle densities U = Lion / (4 π R2 h ν c Ne) in which ν is the energy-weighted mean frequency of the ionizing part of the spectrum of the central source, taken as a point at distance R from the gas under consideration. This ratio ranges from 10-4 for LINER spectra to 0.1 for QSOs and luminous Seyferts. An alternate ionization parameter, the above multiplied by c, is sometimes used, as by Davidson and Netzer 1979 (Rev. Mod. Phys. 51, 715). For a power-law ionizing spectrum of index -1, this gives n(H+)/n(H0) = (U/105.3) for U in cm/s. U is measured from various sets of emission-line ratios, and some estimate of the ionizing continuum may be extrapolated form the optical-UV continuum in Sy 1 and QSO spectra. If the distance is known (you do have a redshift from all these emission lines), the combination via the equation above gives a characteristic scale for the emitting region (usually the NLR).
Emission lines and the far-UV spectrum. Since recombination lines (and a few others) are powered ultimately by parts of the spectrum we can't see directly, they may give our only information on what happens between the UV and soft X-ray ranges. The treatment works like measurement of Zanstra temperatures for nuclei of planetary nebulae: for a nebula optically thick in the Lyman continuum (which they almost always are), the luminosity in a particular emission line is a constant known fraction of that in the Lyman continuum: balancing ionizations and recombinations,
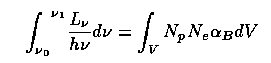
over the emitting volume V. The integration is carried up to a limit set by the amount of helium; an He++ zone will block radiation below (912/4) Å before it encounters much hydrogen. The subscript B denotes case B, the assumption of an optically thick nebula. Since, for example, the Hβ luminosity is
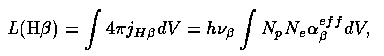
we have in numbers of photons N(Hβ) = N(ion) αeff β/ α B. which gives a fixed ratio between line and continuum intensities. For a given continuum shape, this gives a fixed (distance-independent) equivalent width (with respect to the ionizing continuum's optical tail) (Shuder 1981 ApJ 244, 12; Yee 1980 ApJ 241, 894). Similar arguments may be applied for He II emission, and for a few high-ionization forbidden lines like [Fe XIV] that require lots of far-UV to be produced.
Interaction between UV and optical or IR lines. Several cases are known of line resonance, in which some emission line is stronger than can be produced by continuum processes. The prime example is the O III resonance-fluorescence mechanism found by Bowen. There is a very close coincidence between He II Lyman α at 303.78 Å and a pair of O III lines at 303.62, 303.80 Å. The O III ion is pumped into the upper state by absorption of He II line radiation (depending on local optical depth and velocity field), cascading back to the ground state via a set of about 20 lines in the near UV and optical. These have been seen in a number of Seyferts (e.g. Malkan 1986 ApJ 310, 679), providing some measure of how efficiently He II radiation is converted to O III emission (and thus of a combination of optical depth and velocity shear).
Finally, recall the use of emission lines as kinematic tracers. Thermal motions produce minimal linewidths for a given ion, with a distribution function of line-of-sight velocity
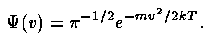
This is small for atoms, and smallest for heavier ones. At 104 K, the 1/e width is 12 km/s for hydrogen and only 4.5 km/s for oxygen. Thus all the structure and widths seen in AGN spectra are from mass motions or some scattering process that can smear frequencies very strongly (a role for electron scattering has been found in a few cases).
The very existence of strong line emission tells us that there must be strong UV radiation from the AGN, and the line ratios tell us that its spectral shape is quite different from a stellar distribution. The line profiles give an obvious distinction between the narrow-line region (NLR) and the broad-line region (BLR) (though there is of course a transition zone, and these are extremes of a continuous gas distribution). The kinematic distinction is mirrored in the densities of these regions; only transitions emitted at high densities (up to 109 cm-3) come from the NLR. We have a general picture of a compact, dense BLR huddled around the core source, and a much more extensive NLR surrounding this and extending in some cases for kiloparsecs. The NLR is spatially resolved in many AGN, with interesting spatial and kinematic structure. Even though it is more distant from the seat of the action, the low density makes classical H II region physics applicable and the interpretation of conditions there less model-dependent than for the BLR.
The Narrow-Line Region. Using straightforward emission-line diagnostics, we may estimate the volume of emitting material: since
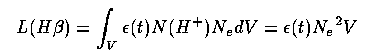
and we estimate Ne ~ 1000 cm-3 from the [S II] line ratio, taking ε = (104) = 8.3 × 1020 gives V ~ 1061 cm³ or a volume 50 pc on a side. Real NLRs are much larger; the Balmer-line surface brightness suggests a volume filling factor of 10-3-10-4. The NLR gas occurs in some kind of clouds or filaments, presumably with a hotter confining medium in between. Since such hot material ablates cooler clouds, we may be dealing with a dynamic situation of cloud production and destruction. Many galaxies have enough gas in their inner region to power a NLR if sufficient ionizing radiation were to appear; in some cases the NLR is probably a pure by-product of the AGN rather than produced by it.
Many recent studies have shown that the NLR is often quite elongated, in the ideal case showing two cones of emission pointing toward the nucleus. This may be seen either in the distribution of emission or in a map of ionization (for example the ratio [O III]/Hβ). These cones show no obvious relation to the galactic disks, suggesting that they mark the regions of ionizing radiation rather than gas presence. From this, it must be the case that the radiation only escapes from the BLR in these directions, perhaps because it is blocked by some kind of torus. This serves as a warning that we don't always see the same continuum as does the gas we are observing, and that extrapolation of the observed continuum into the far UV to estimate the ionizing flux may be wildly inaccurate. These structures are important for "unified schemes" of various kinds of AGN. See the proceedings volume for the ESO workshop Extranuclear Activity in Galaxies, ed. Meurs and Fosbury (ESO, Garching, 1989).
There exist, naturally, transition or intermediate zones between the usual NLR and BLR. This may be manifested as wings on such lines as [O III] λ 5007 or the broader widths of features with high critical density, such as [O I] λ 6300, 6363.
Broad-Line Region. The lines arising here include hydrogen and helium recombination lines, permitted and semi-forbidden lines such as C IV and [C III (most of these in the emitted UV), and complex multiplets of Fe II. The lack of other lines suggests densities in excess of 107 cm-3, and some considerations suggest values as high as 1011. At these densities, recombination is a very efficient radiator; a typical BLR requires only 106 solar masses. The size scale is taken from variability (see below), at as little as a light-week. Line ratios require that the emitting regions be optically thick and heavily stratified - the best bet is again one of fairly discrete individual clouds. One face will be directly illuminated by the ionizing continuum source, with hard radiation penetrating farther into the cloud. A warm, partially ionized zone deep inside the clouds is indicated for heavy-element emission. There will be a skin all around the cloud ionized by reflected UV from other clouds. The number of BLR clouds has been estimated ( > 107) from smoothness of the line profiles. Modelling this requires full-blown radiative-transfer codes. The strictly observational problems produced by Fe II emission are also formidable. As shown in these panels from Boroson and Green (1992 ApJSuppl, 80, 109, courtesy of the AAS) a detailed model for this component is needed before much can be said about either weaker broad lines or the optical continuum shape:
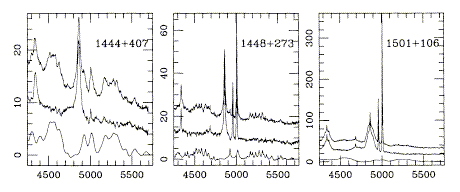
Each cloud in the BLR needs only a fraction of a solar mass. Characteristic velocities are 5000-10000 km/s; variability studies show that velocity structures persist over several crossing times (crossing time of order 6 months). The filling factor of clouds (somewhat depending on assumed density; there are no foolproof diagnostics) is small, so we have once again a lifetime or confinement problem. Two major possibilities are (the standard one of) clouds confined by a very hot medium, and a recurring alternate view in which the "clouds" are stellar atmospheres gravitationally confined. Main-sequence atmospheres are too dense, so one needs either lots of giants and supergiants (Norman and Scoville 1988 ApJ 332, 124; Scoville and Norman 1988 ApJ 33 163) or bloated stars with low-density atmospheres (Mathews 1983 ApJ 272, 390). Detailed understanding of the structure and geometry of the BLR is perhaps best gained from variability studies.
Last changes: 10/2009 © 2000-9