It is widely accepted that there are vast amounts of unseen material in the universe, perhaps 10 times as much as in detectable galaxies and intergalactic gas. What is the evidence? The basic conclusion comes from galaxy rotation curves, mass distributions inferred from hot gas around ellipticals, the velocity dispersions in clusters of galaxies, and mass tracing via gravitational lensing. Not only do we need to know how much of this exists, but where it is - its distribution can distinguish among stellar remnants, hot and cold elementary particles like massive neutrinos or axions,... Recall that most of these techniques are sensitive only to dark matter that is concentrated around galaxies (or more accurately, that galaxies are the marbles rolling up and down hills in dark matter, and that they have had time to fall to the bottom).
The amount of dark matter is often given in relation to luminous material through the mass-to-light ratio M/L, most often taking light at the B band; units are solar masses per solar luminosity. Young stellar populations may have values well below unity; older populations may go as high as of order 10, while the dynamical values for elliptical galaxies and clusters reach hundreds. Since some of the dynamical estimates have the same D2 dependence on assumed distances as does luminosity, the M/L ratio is often distance-independent.
Rotation curves: As discussed in the disk-dynamics section, real disk galaxies show flat rotation curves which require a density distribution approximately scaling as 1/R, so that the mass-to-light ratio M/L rises rapidly into the outer parts of these galaxies. This is known to continue to radii at least 100 kpc from giant spiral galaxies, and probably farther from dwarf companions. For a typical rotation velocity 250 km/s, this gives an enclosed mass of order 1.5 x 1014 solar masses for the biggest spirals, and at least 3 x 1013 for the Milky Way. The magnitude of the problem was clearly set out in a landmark review by Faber and Gallagher (1979, ARA&A 17, 135).
How much of this mass could be in visible matter depends on assumptions such as the lower-mass cutoff of the IMF; if there are enough brown dwarfs, these relatives of normal stars could provide substantial mass and remain very difficult to find. This is why there have been such assiduous searches for brown dwarfs - if the IMF climbs into such low masses, there could be more mass in brown dwarfs than anywhere else. Searches for IR halos around edge-on galaxies suggest that they don't account for all of the problem; there are at least some confirmed local candidates (like Gliese 229B) so we know they exist. The best way to find them wholesale seems to be imaging on and off a methane absorption band in the K window (Jovian planets and brown dwarfs have methane, real stars don't), but IR detectors don't yet allow wide enough fields to search for isolated brown dwarfs. Note that it is precisely the number of isolated ones that is important, since if they're companions to ordinary stars their mass contribution is unlikely to be significant.
The shape of the mass distribution could furnish clues to its nature, and affects the mass estimate somewhat. One sometimes reads of a "disk-halo conspiracy", such that the disk and halo mass distribution are coupled in a way that gives an artificially flat rotation curve that cuts off sharply just at the edge of the measurable region - hence the attempts to get very deep H I maps or use dwarf companions. Carignan and collaborators have produced several examples of dwarf irregulars that must be dominated by dark matter. Still, rotation curves give only lower limits to the total halo mass.
Ellipticals: because these are more kinematically complicated, stellar dynamics has told us less about their total masses. The evidence for massive halos in individual ellipticals comes mostly from the hydrostatic argument, for example giving a total mass of 6 x 1013 solar masses for M87 to a radius of 270 kpc (Fabricant and Gorenstein 1983 ApJ 267, 535). This gives a global M/L ~ 200 in solar units. M87 is an extreme case, perhaps telling as much about the center of the cluster potential as the individual galaxy, but NGC 4472 and 3379 can be shown to require dark matter as well, with spatially resolved temperature profiles. On a more global level, Fabian, Thomas, Fall, and White 1986 (MNRAS 221, 1049) showed that the average temperature and size of the X-ray gas requires M/L=20 for the most conservative assumptions, so that the dark matter must dominate by at least a factor 2, and probably more.
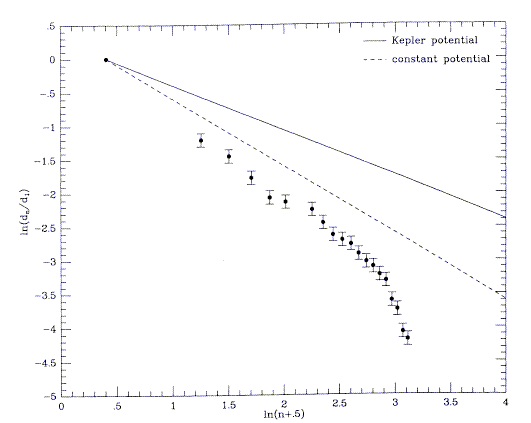
Attempts have also been made to use shells as tracers of the mass distribution in ellipticals. These structures result from merger with a low-mass disk. Since the disk is cold in one dimension, it wraps around the core ("phase-wrapping") and in projection gives sharp-edged shells alternating in sides (Quinn 1984, ApJ 279, 596). Applying a detailed model to the shells in real galaxies, Hernquist and Quinn (1987, ApJ 312, 1) found that the potential is quite deep (global M/L 100-200) and has a larger scale length than the stellar potential. This relies on the fact that the shell spacing is controlled by the potential: from their Fig. 3, for example, reproduced courtesy of the AAS,

Planetary nebulae, pumping much of the radiation into a few emission lines, can be detected out to Virgo even from the ground. This lets us do emission-line kinematics on old stellar populations. The results are a mixed bag; Romanowsky et al. have found evidence that some ellipticals, expecially in tight groups, may be deficient in dark matter compared to typical expectations. On the other hand, some calculations suggest that sampling issues make this a difficult claim to sustain. Stay tuned.
Dynamics of systems of galaxies: this was in retrospect the first real indication of a problem. Zwicky pointed out as long ago as 1937 (ApJ 86, 217) that the velocity dispersion in the Coma cluster was much too high for the suggested galaxy masses. The basic physics here is that a statistically large equilibrium system of particles should satisfy the virial theorem U=-2 E. In practice, one uses observables (radial velocity, position) to estimate E, and compare with some U based on an assumed potential shape (for example assuming that the galaxies fairly sample the potential, which is a reasonable equilibrium situation as long as relaxation among massive objects hasn't segregated visibile and invisible particles). There has been discussion as to the appropriate position variable to give proper weighting. This technique should be perfectly valid for large, dense clusters, since they have (a) many member galaxies, and (b) small crossing times, and are thus likely to be in equilibrium and not still expanding. The virial mass estimator is typically taken as (following Evrard 1987 ApJ 316, 36) and Turner et al. 1979 (ApJ 228, 684):
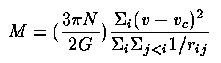
where vc is the cluster mean radial velocity (to be fully correct here one must either use the relativistic recession velocity or correct for another factor (1+z) in the result) and rij is the projected separation between galaxies i and j. There are N galaxies involved.
Claims are sometimes made that the M/L ratio is a systematic function of the size scale on which the measurement is made, usually just before claiming that therefore Ω=1 for the Universe as a whole. Note, however, that different techniques are used for various scales. The real point here is that a technique that applies to systems of a given scale is sensitive only to mass that is clumped on that scale.
Smaller groups of galaxies might probe the mass on smaller scales, but there are uncertainties caused by (1) small-number statistics, (2) the role of interlopers, at all distances, and (3) the possibility that these systems have yet to reach a virialized state, which is hard to define for N<10 anyway. These get worse for binary galaxies; here the derived masses depend critically on how one allows for contamination by nonbound apparent pairs. Karachentsev has made strong arguments for halo masses not much larger than required by present rotation curves.
Gravitational lensing: at last, here is a probe which is unbiased by the luminosity of a target as long as it's transparent. Dark matter is quite transparent; that's the problem. This phenomenon falls out of the principle of equivalence, with a magnitude twice what you would get in a pseudo-Newtonian case assigning the photon a mass hν/c2 (Einstein 1935 , in Science). Zwicky (1937 Phys. Rev. 51, 290 and 679) first suggested that lensing (in some languages more accurately called the gravitational mirage) would be observable on the scale of galaxies, rather than for stars as originally treated by Einstein. The basic equation gives the angular deflection α as a function of impact parameter of the asymptotic line of sight b (note that one has to be very careful about linear measures when geodisics bend) as
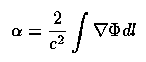
as a vector quantity traversing potential Φ ; for spherically symmetric masses (actually cylindrically symmetric is more nearly appropriate) this becomes a scalar deflection
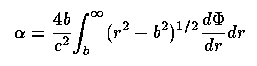
and for a point mass α= 4GM/c2; for a spherically symmetric mass distribution, this is generalized by letting M be the enclosed mass (within the deflected beam) M(b) (not the same as M(r)), following, for example, Refsdal 1964 (MNRAS 128, 295) and Young et al. 1980 (ApJ 241, 507). The obvious integration holds for extended masses, with the approximation frequently possible that b is small compared to the line-of-sight distance. For a more galaxy-like potential with a non-truncated (analytically approximated) King potential of core radius a and central density ρ0.
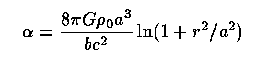
which has a maximum value at b ~ 1.8a of αmax = 45.2 G ρ0 a3 / c2.
Quasars and distant galaxies are both available as probes of lensing masses. Quasars are especially useful for image splitting cases, since we can see them over very long lines of sight and having a proportionally higher chance of being lensed. The fact that the images can be distorted so as to have a larger solid-angle extent (and thus appear brighter) means that if anything we will find the lensed quasars first. For a point-mass lens, the amplification is given by

where r is the impact parameter in units of c /4 (GMD)1/2 for a lens at proper distance D. One can predict the distribution of image splittings for a given galaxy mass spectrum (Turner et al. 1984 ApJ 284, 1), and if we go by luminous masses almost all lenses should have splittings in the 0.1-arsecond range. Known and strong candidate lenses mostly have splittings 2-7 arcseconds, and an HST snapshot survey (Maoz et al. 1993 ApJ 409, 28), along with lots of VLA survey work, have so far failed to reveal any new small-splitting lenses. The current lensed QSO list is sneaking up on 100 as the SDSS harvest is reaped; some of the classics include:
| ID | zQSO | zlens | splitting | images | discovery | notes |
| 0957+561 | 1.4 | 0.36 | 5.7 | 2 | Walsh, Carswell, Weymann 1979 Nature 279, 381 | "the" double QSO |
| 2345+007 | 2.15 | ... | 7.1 | 3? | Weedman et al. 1982 ApJL 255, L5 | ... |
| 1115+118 | 1.72 | 0.31 | 0.4-2.3 | 4 | Weymann et al. 1980 Nature 285, 641 | "triple QSO" |
| 1634+267 | 1.96 | ... | 3.8 | 2 | Spinrad & Djorgovski 1984, ApJL 282, L1 | ... |
| 2016+112 | 3.27 | 0.24 | 3.4 | 3 | Lawrence et al. 1984, Science 223, 46 | not a QSO |
| 2237+030 | 1.69 | 0.039 | 1.3 | 4 | Huchra et al. 1985, AJ 90, 691 | the "Einstein cross" |
| 0142-100 | 2.72 | 0.49 | 2.5 | 2 | Surdej et al. 1987 Nature 329, 695 | UM 673 |
| 1413+117 | 2.55 | ... | 1 | 4 | Magain et al. 1988 Nature 334, 325 | the "Cloverleaf" |
| 10214+4724 | 2.3 | 0.7? | 0.7 | arc | Eisenhardt et al. 1996 ApJ 461, 72 | ... |
| 1120+019 | 1.47 | ... | ... | 4 | Michalitsianos et al. 1995ApJ 439, 599 | UM 425 |
| 1422+231 | ... | 0.34 | ... | 4 | Impey et al. 1996 ApJL 462, L53 | ... |
| 1208+1011 | 3.8 | ... | 0.48 | 2 | Bahcall et al. 1992 ApJL 392, L1 | ... |
| B1359+154 | 3.2 | 1.0 | 2.0 | 6 | Impey et al, did they publish??? | Six images, three lens galaxies |
A number of similar candidates still lack confirming spectroscopy or high-resolution imagery, and some beautifal radio rings are omitted. A current list is maintained by the CASTLE group. The large splittings suggest that masses of cluster magnitude, rather than single galaxies, must dominate the statistics, and that these masses are in the neighborhood of 1014 solar masses. By now, the pattern of 3-4 small blue objects around a larger red one is often taken as presumptive evidence of lensing (as in the MDS fields, Ratnatunga et al. 1995 ApJL 453, L5).
A topological theorem (e.g. Burke 1981 ApJLett 244, L1) states that nonsingular mass distributions produce odd numbers of images. Apparently the last one is frequently very faint. Note the difficulty of being certain that one is dealing with multiple images of the same quasar in very wide pairs. The classic case is that of 1146+111, trumpeted widely by Turner et al. 1986 (Nature 321, 142) and other papers in the same issue as a case of lensing by a cosmic string, only to be retracted (basically by the editor) when further data showed spectroscopic differences between the components.
Aside from global constraints on α and A, detailed models are possible when the lens galaxy or cluster can be identified, a redshift and velocity dispersion measured. and perhaps shear in the lens field measured (for example by VLBI mapping). In the well-observed 0957+561 system, there is some evidence that not only does the cluster have huge unseen mass, but that it is not quite concentric with the galaxy distribution. There are now several proceedings devoted to gravitational lensing, where reviews may be found: the 1984 Liege meeting (Quasars and Gravitational Lenses) and Gravitational Lenses edited by Moran et al. (1989, Springer-Verlag) from a meeting at MIT. Also of interest is Dark Matter in the Universe, ed. J. Bahcall et al. (World Scientific, 1987).
A generalization of the gravitational lens technique uses large numbers of faint background galaxies to probe the cluster potential. This was first tried for individual galaxies by Tyson et al. (1984 ApJLett 281, L59), and given new impetus by the discovery of luminous arcs in galaxy clusters (Lynds and Petrosian 1986 BAAS 18, 1014; Soucail et al. 1987 A&A 172, L14; 1988 A&A 191, L19). The redshifts of the arcs (an impressive feat) are much higher than the clusters, implicating gravitational lensing. Statistical models have been very successful in reproducing the occurrence and appearance of the arcs (as in, for example, Grossman and Narayan 1989 (ApJ 344, 637). The arcs in Abell 2218 show the effect quite intuitively (as discussed by Kneib et al 1996 ApJ 471, 643 and Smail et al 1996 ApJ 469, 508). This image is from the HST SM3A OV phase (how's that for stacked acronyms?). Notice the divergence of arcs around the bright galaxy to the lower left, showing that there is a significant concentration of total mass associated with it rather than just the cluster as a whole.

A remarkable extension was introduced by Tyson et al. (1990 ApJLett 349, L1) who analyzed the images of faint galaxies around nearby clusters statistically and were able to derive not only masses but the mass distribution. Color selection allowed discrimination between faint cluster members and the distant background galaxies that will show this distortion. This approach, so-called weak lensing, can also be used statistically for individual galaxy masses. They find that the matter is only slightly more extended than the galaxy distribution; the dark matter in these cases is associated more with the cluster as a whole than with individual galaxies (see the work by Whitmore et al. on rotation curves in clusters for more ramifications). The lensing mass distributions for two clusters are shown in their Fig. 4 (courtesy ofthe AAS):
Further applications of this effect include microlensing - the amplification of a compact source (i.e. QSO core) by individual stars in the lens galaxy, with very small impact parameters. This could lead to variability on timescales of a few years (Canizares 1981 Nature 296, 397, for example). This must in general be treated statistically, and gives a fundamental limit to how well we can determine lens parameters from any observations of finite length. Note Canizares' introduction of an elegant technique for calculating gravitational image properties based directly on Fermat's principle.
The same lensing calculations also apply locally, forming the heart of several massive projects aimed at seeing what the contribution of white dwarfs, red dwarfs, brown dwarfs, and loose "rogue" planets is to the Milky Way's mass. These - such as MACHO, OGLE, EROS, AGAPE, MOA - use stars in the LMC or galactic bulge (for AGAPE, in M31 via what's known as pixel lensing) as background sources and watch for the characteristic shape of a lensing event as foreground point sources transit in front, while maintaining constant color. This is an unlikely event, so 106-107 stars need to be followed to see a few events per year. Events are seen at this rate, and some show the distinctive signatures of binary lensing. This approach tells us how much mass in the Galaxy's halo (and between here and the bulge) consists of compact objects massive enough to lens background objects as big as stars; as an upper bound, an isolated Jovian would produce a projected Einstein radius a bit smaller than a red giant appears in the LMC, while planets could in principle have strong effects on the lensing by the parent star. Here's an example of a lensing event against an LMC star, from the MACHO WWW site. Important characteristics that make a brightening of some star image a microlensing candidate are that it be achromatic (since gravitational lensing doesn't have chromatic aberrations), and that it be symmetric and follow that predicted amplification history of a straight slice moving through the Einstein radius. While more complicated situations are possible (binary or resolved lenses, apparent motion interacting with the Earth's orbit) all these require excellent data to find. At this point, the otherwise uncatalogued mass in the Milky Way has a nontrivial but likewise non-dominant component in dim stars and stellar remnants. The publications to date have been a bit cagy with exact numbers, but one report by the MACHO groups puts the amount of baryonic dark matter in stellar remnants of about 0.5 solar masses at about 20% of the dynamical mass, with less massive objects comprising a much smaller fraction.
Gravitational lenses can also (again in principle) give the Hubble constant. This requires a measure of lens mass that has a different dependence on distance than does α itself, such as a cluster velocity dispersion. Rhee has done this for the 0957+561 lens cluster, claiming H0 = 42± 17 km/s from this single observation, while a recent compilation of available time delays gives a value near 70. The best measure of mass scale in the lens is the differential time delay between the light paths, measurable when the background QSO is appropriately variable. The QSO 0957+561 seems the best case so far, with the delay pretty well constrained at 1.3 years; Schild has found that microlensing which must be from planetary-mass objects in the main lens galaxy complicates the timing analysis but is at least as interesting from a mass standpoint.
Primordial nucleosynthesis and q0: the relative primordial abundances of H, D, He, Li, and Be are predicted by a simple Big Bang model, since the universe from times 3-11 minutes was almost perfactly flat and the rate of neutron capture therefore depended on the baryon density. Observed abundances in old stars and pristine gas imply the the baryonic mass density of the Universe is only 7-10% of critical density - well below what is required for the total by galaxy and cluster dynamics. This may be telling us that the remainder is non-baryonic (exotic particles), with matter locked in black holes a wild card depending on whether they were formed before or after the epoch of nucleosynthesis. There will be more on primordial nucleosynthesis later in the course.
Alternative explanations: it is puzzling that it took several years for anyone to seriously discuss the possibility that the fault lay not in the stars but in ourselves - that perhaps our understanding of gravity is faulty on such large scales. Milgrom (1983 ApJ 270, 365; 270, 371; 270, 384 and subsequent papers) took up the idea with vigor, proposing that there is a minimum gravitational acceleration somewhat by analogy with the quantum behavior of particles. Tests on galaxy rotation curves look bad for the idea, but Milgrom claims they are still inconclusive. Still, someone needed to examine this possibility, and the fact that it took about 5 years doesn't speak too well for the astronomical community.
A recent result which has attracted much attention, as possibly resolving the issue in favor of actual dark matter, is illustrated below from HST/Chandra/Magellan data by Clowe et al. This galaxy cluster, 1E0657-56 (the Bullet Cluster) has long been seen to show evidence for being two dynamical systems in the throes of merging. Models indicate that the hot X-ray gas should undergo strong dissipation, while dark matter and te relatively small galaxies would fly apart at least temporarily after initial passage through each other. The X-ray gas (pink) indeed stayed put between the two galaxy clouds. Gravitational lensing of deep background objects shows that the mass distribution (blue) stayed with the galaxies. Since the hot gas dominates the baryonic mass in such rich clusters, this is strong evidence that the material in clusters is indeed some kind of invisible material, weakly enough interacting to suffer no significant disruption when clusters pass through each other.

How many kinds of dark matter are there? Theory makes a convenient distinction between hot and cold dark matter, where HDM is relativistic and therefore doesn't fall easily into galaxy-sized potential wells, and CDM ends up with the dynamical properties of tracer particles just as stars do. Neutrinos would be hot unless their rest mass is higher than experiment now indicates, and the often-hypothesized weakly interacting massive particles (WIMPs, as contrasted to MACHOS = massive compact halo objects) and other baryonic forms would be cold. The implications for galaxy formation are rather different, and some bold workers suggest that a mix is required. Baryonic dark matter would be cold, as would massive enough neutrinos. While it seems to violate Occam's razor, there is compelling evidence for both baryonic and nonbaryonic dark matter. There is a strong theoretical prejudice, driven by inflationary cosmologies, that there be enough nonbaryonic material to give closure density (q0 = 1/2), but regardless of the amount it is important in galaxy formation. Nonbaryonic dark matter need not have been coupled to radiation before the epoch of recombination, and could therefore have clumped gravitationally while ordinary matter was still as smooth as we see the microwave background to be. In this scheme, the DM fluctuations seeded galaxy formation to occur much faster than might otherwise have been the case. Locally, dim enough stellar remnants count as a form of dark matter (as for that matter did Sirius B and Neptune before their visual identification), and in fact it is this component that the gravitational-lensing surveys see. As we've seen, molecular gas, and for the intergalactic medium highly ionized gas, have enjoyed brief periods of vogue as candidates for significant amounts of baryonic dark matter.
Last changes: 2/2015 © 2000-15