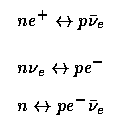
There are several recognized processes from the early universe that leave relic effects setting the stage for galaxy formation and evolution. We deal here with the first generarion of stars, primordial nucleosynthesis, the epoch of recombination, and the thermal history of various cosmic backgrounds.
Several kinds of evidence point to an early (pregalactic) source for a small level of enrichment in heavy elements (especially, at this point, oxygen). These include the patterns of abundances in extreme Population II stars in the Milky Way and the O/H ratio in intergalactic gas. This early enrichment may be the first evidence of the first generation of stars, variously known as Population III, very massive stars (VMOs), or very massive objects (VMSs). They must have been able to form in a way different from what we see in today's Universe, without any dust or heavy elements to assist in cooling the gas during collapse. This would tip the typical masses to much greater values.
Cooling at zero metallicity can proceed only through radiation from lines of molecular hydrogen (including its deuterated form HD), which will form at very low concentrations in the pregalactic Universe. It is important that the "neutral" Universe still had an ionized fraction of order 10-4, since this facilitated formation of molecules through a charge-exchange reaction (recently detailed by Abel et al. 1997 NewAstron 2, 181) starting with
This weakly-bound ion then forms H2 via
so that it is proper to speak of the free electrons as catalysts. The H2 and HD molecules can cool through radiation in rotational and vibrational transitions lying in the near-infrared, down to temperature around 200 K (where the cooling is slowest). This temperature defines the mass scales on which objects can collapse if only this molecular cooling operates; the temperature is several times higher than the ultimate limit from equilibrium with the "microwave" background temperature seen by an object at redshift z, of 2.7 x (1+z) K.
Several recent numerical studies (Abel, Bryan, & Norman 2002 Science 295, 93; Bromm, Coppi, & Larson 2002 ApJ 564, 23) have converged on the results of such a collapse. The first stars were massive, hot, and efficient at enriching their surroundings in processed elements. The restricted cooling possibilities mean that only masses in the rough range 80-300 solar masses formed these stars, without further fragmentation as we see today. The lack of opacity from heavy elements made them substantially hotter than even comparably massive present-day stars, and copious emitters of Lyman-continuum photons. Not only did they ionize their surroundings, albeit briefly, but this radiation dissociated the H2 and HD throughout their ancestral clouds, so that these stars formed one to a "galaxy".
A first-generation star of given mass was hotter than any later star of the same mass. With no elements to engage in the CNO cycle on the ``main sequence", core fusion proceeded by the p-p chain, driving the core temperature to ~108 K to balance the pressure of the large masses (Tumlinson & Shull 2000 ApJLett 528, L54; Tumlinson, Giroux, & Shull 2001 ApJLett 550, L1). For chemically homogeneous stars, a hotter core also means a hotter surface.
There is less agreement among models about the exact nucleosynthetic yield and abundance pattern of the material returned to the intergalactic gas by the final explosions of these stars, largely driven by the considerable differences in supernova machanism with mass and the strong senstivity of the outcome to details of envelope ejection (the so-called mass cut, the point in a stellar envelope beyond which all the material is taken to escape the compact remnant, which probably has to be properly treated as more than a single cutoff value). Broadly, tens of solar masses of ejected material can be released from such an explosion. Details depend strongly on the mass distribution of the stars, both in the nucleosynthesis and because they may undergo different kinds of supernova explosion at different masses. Such exotic mechanisms as pair-production instability or reverse nucleosynthesis can drive core collapse in various mass ranges. The most massive stars, above about 260 solar masses, may swallow their entire masses into black holes rather than produce supernovae. In contrast, the pair-production collapse occurs for masses 140-260 solar masses, resulting in intense nuclear burning and completely disrupting the star (Heger and Woosley 2002 ApJ 567, 532). The relative amounts of heavy elements they produce, and expel to the surrounding medium, can depend strongly on the stars' mass distribution.
Since they occurred singly rather than in clusters, and are individually short-lived, detection of these stars during their normal lifespans will be beyond our means for some time. However, their supernova outbursts may be an order of magnitude more luminous than the type Ia supernovae that can now be discovered to at least z=1.7, and for the redshift range z=10-30 where we expect to see such objects, the peak flux is almost constant with redshift. They should reach a peak AB magnitude near 26, with the redshift determining what wavelengths we could detect them in (through absorption shortward of Lyman α from the neutral IGM). Time dilation improves the odds of detecting such explosions, since the observed outburst may last for several years. If, for example, 10-6 of the baryons were incorporated into these first stars, we would see a supernova explosion from this population every 6 seconds somewhere on the sky (Heger et al. 2002, Lighthouses of the Universe, p. 369). This flux level in the K band, corresponding to supernova redshifts z < 17, is in principle detectable now with such instruments as the Keck telescopes, but not over wide enough areas to find these explosions by blind search. For larger redshifts, the thermal background for ground-based instruments makes their detection even more difficult, and a prime task for JWST. Searching for these supernovae (or hypernovae) suggests that deep fields, such as those to be observed by JWST, are most effectively built up by observations spread in time across a couple of years.
Ironically, we may be already observing some of these supernovae, while remaining ignorant of the fact. The connection between gamma-ray bursts and supernovae is enticing (some might say "seductive") based on the properties of the long-wavelength afterglows, composition of hot gas in the afterglows from X-ray spectroscopy, location with respect to host galaxies, and calculations of stellar implosions which can produce a temporary accretion structure around a young black hole (reviewed by Mészŕros 2002). If these more massive stars had similarly asymmetric explosions, which would include temporary formation of disks around young black holes, they should produce gamma-ray bursts as well over an appropriate solid angle. The striking lack of a fluence-redshift relation for bursts with identified host galaxies might mean that some fraction of the bursts already being observed, and for which we cannot identify a host galaxy, may lie at substantially higher redshifts.
These earliest stars played a crucial role in setting the stage for the "normal" star formation to follow. Even a tiny salting of heavy elements changes the cooling of interstellar clouds and the properties of the resultant stars dramatically. As soon as the mean metallicity of cooling gas rose above ~10-8 by mass, the nature of star formation switched to nearly what we see today, reflected in the extreme Population II stars still extent in our neighborhood.
The strongest constraint on the number and metal yield of these stars comes from the minimum metallicity encountered anywhere. It is not clear yet just what the distribution of stellar metallicity in the Milky Way is at the low end. There are several stars known with [Fe/H]~-4, and one at -5.3, found from winnowing thousands of candidates starting from broad-band colors or slitless-spectrum line strengths. The value of 10-4 solar is broadly consistent with the carbon abundance seen from co-adding large numbers of systems in the Lyman α forest (Cowie and Songaila 1998 Nature 394, 44, Ellison et al. 2000 AJ 120, 1175) although the oxygen abundance may be an order of magnitude greater (Telfer et al. 2002 ApJ 579, 500). The abundances in low-density intergalactic regions are especially important, since these are unlikely to have been enriched by supernova ejecta in galactic winds as we see them in starburst systems today (Ostriker and Gnedin 1996 ApJLett 472, L63). The recent detection of widespread O VI absorption from the cosmic web shows that enrichment took place over large regions, although the very uncertain ionization corrections, and easy detection of O VI in shocked regions where matter is falling into denser concentrations, make quantitative abundance estimates difficult (Tripp, Savage, & Jenkins 2000 ApJLett 534, L1).
Finally, in connecting the products of the first stars to what we see in old populations today, we need to establish how homogeneous the mixing of their products was, and on what scales it occurred. This enters into what their overall nucleosynthentic signature is on extreme Population II stars. For example, should we consider their output to account only for the most metal-poor stars, as in the example at [Fe/H]=-5.3, or could our Galaxy have formed from gaseous regions that experienced such differing levels of early enrichment that the stars near [Fe/H]=-4 also bear their imprint? A hierarchical buildup of the Milky Way could allow it to contain stars originally in rather different chemical environments, if the dispersal of metals from primordial stars was uneven enough.Some of the complexities of applying this idea to the galactic abundance distribution are considered by Oey (2002 Astrophys Space Sci 281, 483).
Primordial nucleosynthesis led to to chemical properties of the first generation of stars, perhaps also affecting the cooling rate at early times. Production of heavy elements (mostly He) resulted from competition between fusion, the expansion, and neutron decay. At very high temperatures, thermodynamic equilibrium and detailed balance give equal numbers of protons and neutrons. Calculations of his kind date to Gamow (1948 Phys. Rev. 74, 505), Alpher and Herman (1949 Phys. Rev. 75, 1089), and Hayashi (1950 Prog. Theor. Phys. 5, 224). A recent critical comparison of reaction rates and results is given by Walker et al 1991 (ApJ 376, 51); see also the compact treatment in section 7.5 of Zel'dovich and Novikov. At high temperatures, such that the rates for n<-->p reactions
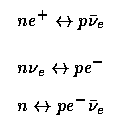
are faster than the expansion timescale t = 1/(2H), the neutron/proton ratio follows its equilibrium value
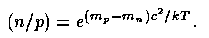
At temperatures below about 1 MeV, the ratio freezes as the expansion decreases the density of available particles for two-body processes. To calculate expected abundances, one uses the expansion history for a particular set of cosmological parameters and follows the possible reactions for mass number 7 and less, such as
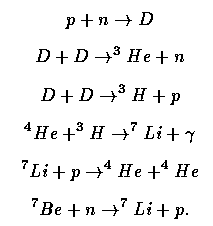
As in stellar cores, the mass gap at mass number 8 is bridged in negligibly small numbers. The major uncertainties in the calculation have been in nuclear reaction rates at the relevant energies, and in the free neutron half-life τn ~900 seconds. Unlike stellar cores, there is an important population of neutrons; otherwise the reaction to make D would be far too slow. The nucleosynthesis period effectively begins when the characteristic photon energy is too low for photodissociation of deuterium, which is at T ~8 × 108 K. We should all be happy that it is not too different from this because there would either be all heavy elements or none if the cooling timscale were too different from the neutron half-life.
The relevant data for comparison come from old stars or H II regions in apparently pristine regions. There is some dispute on how to account for stellar contamination in later nucleusynthesis. The helium mass fraction YP is close to 0.23, consistent with a baryon density of order 10% of critical density; the density of baryons alone is measured in this way (see Yang et al. 1984 ApJ 281, 493 for the approach). Typical predictions of the helium abundance YP as a function of q0 give
| q0 | 2 | 0.2 | 0.02 |
| YP | 0.27 | 0.25 | 0.23 |
We may derive a mean mass density at the present epoch by using all the light species together, for example in the recent review by Olive, Steigman, and Walker (2000, Phys. Reports 333-334, 389). See also Vangioni-Flam, Coc, and Casse (2000 A&A 360, 15) for a review and update of the input nuclear reaction rates. This figure, from Yang et al. courtesy of the AAS, shows how different isotopes give different kinds of density bounds:
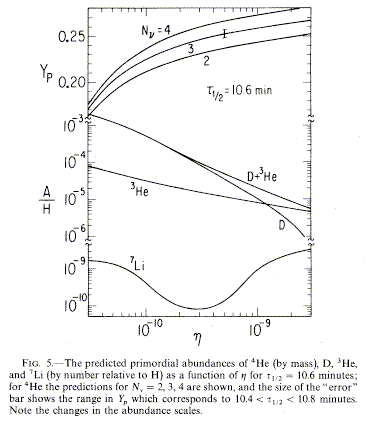
Primordial nucleosynthesis also depends on the number of flavors of neutrino; the more there are, the more neutrons will be produced in the early universe and the more helium will remain. The value above implies only three kinds of leptons, fortunately allowed by the three known generations. Other nuclei provide better constraints on density, hence the excitement over looking for deuterium in the atmospheres of giant planets and in QSO absorption-line systems.
Before recombination matter and energy are strongly coupled by scattering - the density is high enough to approach thermal equilibrium. The epoch of recombination may also be called the epoch of decoupling. As long as these components are linked, the time t and temperature T are related by t = 3c² / (32 π G a T4)1/2, a relativistic result derived via radiation density. For radiation, the energy density goes as 1/R4, while for matter it goes as 1/R³ the different behavior gives a change in state as space expands. The observed CMB temperature is set by the fixed temperature at which hydrogen recombines (about 14,000 K) and the redshift at which this happened, since a blackbody changes its observed temperature as 1/(1+z). Thus a temperature of 2.735 K implies a redshift for this epoch of about 1000 and mass density 109 times its present value. It is interesting that the present average energy densities in the CMB, cosmic rays, and starlight from galaxies are comparable.
Distant galaxies, especially AGN, have been used test the uniformity of physical laws. The idea is that we can see sets of distant AGN which would never have been causally connected under a standard big-bang picture, and that it is puzzling that such disconnected regions have identical physical constants and laws as interpreted from spectral features. This was one piece of evidence leading to the acceptance of inflation. Ratios of wavelengths in QSO absorption-line systems have been used to set tight limts on variations of such quantities as the fine-structure constant α = 2 π e2/hc; Webb et al (2003 ApSpaceSci 283, 565) and Murphy et al. (2003 ApSpaceSci 283, 577; 2001 MNRAS 327, 1223 and 1237) have argued for a small change to z=3 or so, at the level of 10-4. This would be a big deal for cosmology and fundamental physics if it pans out.
Last changes: 11/2009 © 2000-9