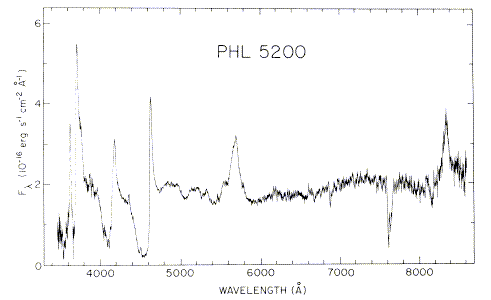
Some QSOs show very broad blueshifted absorption troughs associated with strong UV resonance lines. The type example is PHL 5200, shown in Fig. 1 of Junkkarinen, Burbidge, and Smith 1983 (ApJ 265, 51, ADS by permission of the AAS):

The properties of these systems have been reviewed by Weymann, Turnshek, and Christiansen 1984 (in Astrophysics of Active Galaxies and Quasars, p. 333), Weymann and Foltz 1983 (Liege Astrophysical Coll., p. 538), Turnshek 1984 (ApJ 280, 51) and Turnshek 1988 (in QSO Absorption Lines; Probing the Universe, p. 17). Salient features of these spectra include:
Broad absorption lines are direct evidence of outflow from AGNs, at very respectable velocities. The primary questions are then (1) what is this absorbing region and (2) is the BAL phenomenon an intrinsic property of a few QSOs or do most QSOs look like this if viewed from certain directions?
The BAL region is likely broadly similar in scale to (if necessarily a bit larger than) the BLR - the velocities, occurrence of excited states in absorption, and lack of absorption from such transitions as [O III] all suggest this. If the phenomenon is intrinsic, the covering factor of this cloud population is near unity, while if it is an orientation effect, the covering factor is of order the ratio of BAL QSOs to all QSOs in a mythical unbiased sample (as high as 10% if typical sets of QSOs are representative). The flow (or clouds) must be at least slightly outside the BLR since some broad lines are strongly absorbed. Correlations between BAL occurrence and line profiles in N V indicate that some of the BLR is coextensive with the BALR. Radiation pressure is a popularly invoked driver for the outflow, though it is still not clear whether the flow is accelerating or decelerating across the region we see. That is, the question is whether the highest velocities are at the inside or outside of the flow. Answering this is confused by the role of changes in the ionization state and pressure balance of the absorbing material (which may or may not comprise most of the outflowing matter; Arav et al. 1994 ApJ 432, 62). One issue which has gone in and out of fashion repeatedly is line locking, which would accelerate gas to certain "magic" velocities and then keep it there based on having strong line features in the absorption cross-section of the gas.
The individual absorbers are not very small, as no profile changes have been observed over 15 years or so of high-quality data for PHL 5200; note, however, the report by Barlow 1994 (PASP 106, 548) of changes in the depth (though not velocity structure) of the features apparently linked to continuum/ionization changes in several BAL objects. This favors large clouds or a smooth wind. The distinction may blur, as various BALs have profiles that range from smooth or highly structured. It is not obvious which way the velocity-position mapping goes, or whether the flow accelerates or decelerates outward. The material is highly ionized (neutral H column density less than about 1016 per cm² to avoid stronger Lyman α effects).
Major outstanding problems include:
Wind and cloud models have different successes and problems. Winds don't get ionization levels even approximately, don't naturally have fine velocity structure, and don't easily give velocity-detached BALs. Clouds have less trouble with ionization levels, but clouds of reasonable size would evaporate quickly.
A few Seyfert nuclei also know how to do this gas-acceleration trick. The heavily obscured nucleus of Mkn 231 is renowned for multiple optical absorption systems covering a wide span of redshift.
A few objects show clear signs of inflow of material, always a good sign if we want to seriously discuss accretion power. There is a supposition that inflow and outflow may coexist in one object in different pieces of solid angle around the core source. Redshifted absorption lines of H I and OH have been seen toward the nuclei of Cen A (van der Hulst et al. 1983 ApJLett 264, L37; Seaquist and Bell 1990 ApJ 364, 94) and other radio galaxies (van Gorkom 1987 in Structure and Dynamics of Elliptical Galaxies, IAU Symp. 127, p. 421). They may have appreciable velocity width, as shown in Fig. 1 of Seaquist and Bell (courtesy of the AAS:
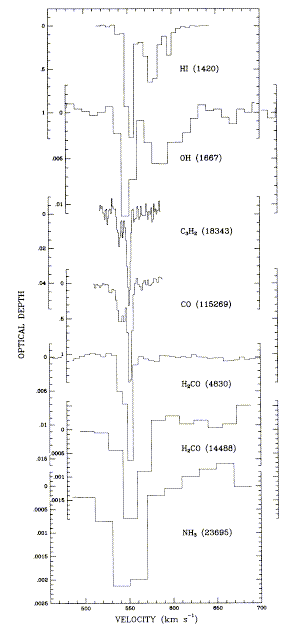
These observations are crucial in clearly showing gas moving inward. It is not always clear how this relates to accretion - modest inflow velocities can be attained via orbital dynamics in some situations without coming close to the nucleus. Also, the net inflow needed to fuel the nucleus may be very tiny at large radii and easily lost in the details of galaxy dynamics. One glaring example of this is in seeking bar-driven gas flows. Bars and oval distortions will populate orbits along the bar, and the observed velocities from such flows are very large compared to net inward streaming of gas as it loses angular momentum to collisions. Thus its kinematic signature will be swamped. Quillen et al. (1995 ApJ 441, 549) have used the 1/r nature of the gravitational potential and K-band imaging to estimate the potential shape and infer the inflow rate from calculated torques on the gas-rich dust lanes in a few nearby bared spirals, pointing to one avenue that can (more or less) measure mass inflow on kpc scales.
By default, accretion power is the only way to generate AGN luminosities in the required small volumes for interestingly long times. A fiducial value for the expected maximum luminosity from accretion is the Eddington limit. This is the luminosity at which, for uniform spherical accretion, the radiation pressure on accreting material balances the gravitational force and thus stops further accretion. In the case of zero angular momentum material falling at distance r onto a central object of mass M, the radiation pressure per unit infalling mass is κL / 4 πr² c. Here κ is the absorption coefficient per unit mass; at high temperatures one takes the electron-scattering coefficient, and c accounts for momentum transfer. The Eddington luminosity is thus, in this regime,
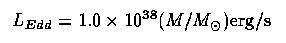
Thus, AGNs with bolometric luminosities up to 1047 ergs/second may need central masses up to 109 solar masses. Some nearby weak AGN with dynamical evidence for large central masses must then by somewhere around 10-4 of the Eddingtojn luminosity, a difference which has sometimes been invoked to distinguish objects in active accretion form those which may be powered mostly by something like extraction of energy from the angular momentum of the central object.
In real AGN spherical accretion is not reasonable; gas in galaxies will have some net angular momentum, and the transverse veliocity is amplified during infall. If the accretion rate is high enough for collisions, and accretion disk will form (basically what planetary rings are). Physics of these disks is still poorly understood. It is known that the Eddington limit may be exceeded by a factor of a few in nonspherical accretion (the material may shield itself and not be exposed to most of the radiation), time-dependent accretion rate, or anisotropic radiation patterns.
Accretion disks. This is the normal steady-state accretion configuration for astrophysical objects. Mass moves inward at a rate set by the outward transport of angular momentum, regulated by the viscosity (generally speaking). The details of viscosity are very poorly known. It is popular to treat an "α-disk", in which the viscosity is α cs H where cs is the local sound speed and H is the disk thickness, and α < 1. See Pringle 1981 (Ann Rev A&A 19, 137) and Frank, King, and Raine, Accretion Power in Astrophysics.
The disk structure is determined by various conservation equations. Take a cylindrical coordinate system r, φ, z with equator along the disk. The radial momentum flow is governed by
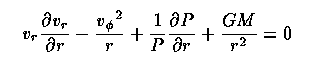
or incorporating the sound speed cs and Mach number m,
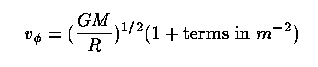
Hydrostatic equilibrium gives no net flow in the z-direction:
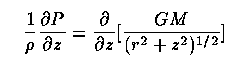
at density ρ. For a thin disk, this approaches -GMz/r³ so the disk thickness will be H ~ r/M.
The mass flow rate (accretion rate in a steady state) must by mass conservation be constant with radius
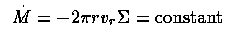
where Σ is the local surface density (integrated over z).
The disk thermal luminosity is the same as the internal dissipation rate (conservation of energy)
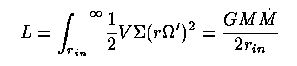
where V is the viscosity; the term in parenthesis is angular momentum. Half the rest energy remains at the inner edge of the disk. If each part of the disk surface radiates as a blackbody,
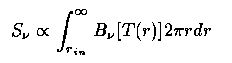
which results in a ``fat" blackbody spectrum. This has an exponential falloff at high frequencies, a characteristic slope ν1/3 at intermediate frequencies, and drops as ν² at low frequencies on the Rayleigh-Jeans tail.
These considerations are complicated not only by our ignorance of the detailed physics, but by geometrical factors. If radiation is inefficient compared to dissipation, the disk may puff up into a "Polish doughnut" (Abramowicz et al 1978 A&A 63, 209). This must be treated as a stellar structure problem. This gives funnels, a naturally interesting place to make jets. These are so deep that we might not expect a clear view of the core itself. Disks may also generate winds and coronae that could produce some of the observed emission. Finally, if the angular momenta of the central object and accreting gas are misaligned, the disk may twist, precess, or exhibit damped oscillations.
The shortest obvious variability scale for an accretion disk is related to the rotation period at the inner edge, which is thought to be approximately the radius of the last stable orbit (about 2 Schwarzschild radii):
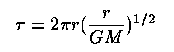
at the inner edge. A timescale of 1000 seconds then implies a mass 1.1 × 1040 g or 5.7 × 106 solar masses.
Last changes: 10/2009 © 2000-9