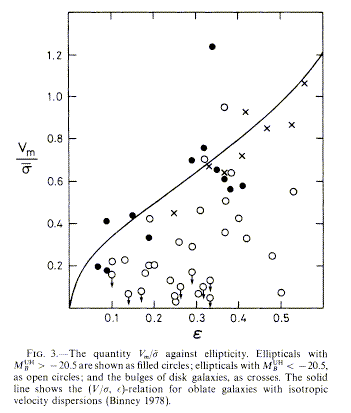
For decades it was considered obvious beyond the need for observations that elliptical galaxies were oblate objects, rotationally flattened. The observations to actually check this were quite difficult, since ellipticals don't have convenient numbers of H II regions, but revealed that most ellipticals rotate far too slowly for their apparent shapes - the shape must be an intrinsic property of the stars' velocity distribution (see Davies et al. 1983 ApJ 266, 41). An important discriminant is the ratio v/ σs of rotation velocity to (line-of-sight) velocity dispersion. For a given shape of potential, v/ σ predicts flattening ε. Elliptical galaxies mostly ignore this prediction, leading to the notion that their shapes are triaxial ellipsoids supported not by rotation, but by anisotropy in the velocity distribution of the stars. This is shown in Fig. 3 of Davies et al. (shown courtesy of the AAS):

To model these galaxies in detail, one must consider statistical mechanics of available kinds of orbits (tube, box...) and their stability - see Binney and Tremaine ch. 2-5). In general, one expects orbits in such a family (in either physical or phase space) to obey the ergodic theorem, so that a star will eventually approach arbitrarily close to any specified point within the envelope of its orbital family. This approach of loading orbit families, to get a self-consistent set of orbits and potentials, has worked better for shapes than M/L ratios. The behavior of σ(r) at small radii contains information on the degree of central mass concentration (is there a supermassive black hole?), but even here anisotropic velocity dispersion can complicate the analysis, as seen in the controversy over the core of M87. Sargent et al. 1978 (ApJ 221, 731) and Young et al. 1978 (ApJ 221, 721) announced with great fanfare that M87 had a black hole with billions of solar masses, on the basis of a concentration of starlight at the center and a rise in velocity dispersion (shown in Fig. 4 of Young et al, courtesy of the AAS):
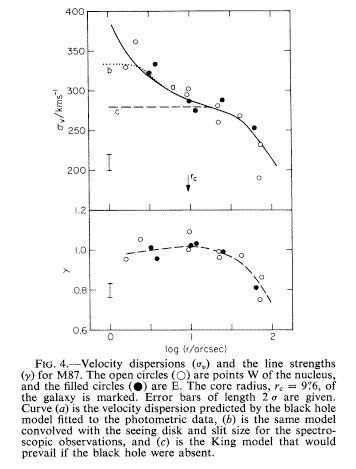
Richstone and Tremaine 1985 (ApJ 296, 370), following work by people such as Duncan, showed that a sufficiently anisotropic velocity distribution of the stars could mimic this result, but there are stability problems with the long-term survival of extremely anisotropic dispersions. There has been more recent work on just how high the central velocity dispersion climbs (Dressler and Richstone 1990 ApJ 296, 370, for example). Looking for resolved peaks in velocity dispersion has become a cottage industry (M31/M32, Tonry 1987 ApJ 322, 632, Kormendy 1988 ApJ 325, 128, Dressler and Richstone 1988 ApJ 324, 701; M81, Keel 1989 AJ 98, 195; M104, Jarvis 1988 A&A 201, L33) so that people wouldn't be terribly surprised if black holes turn out to be common in galactic nuclei. High angular (linear) resolution is a must here, to distinguish between a relatively low-mass but tiny stellar core and the more extensive gravitational influence of a supermassive object. Remember in these cases that we measure the one-dimensional velocity dispersion along our line of sight - this is related to the three-dimensional dispersion by the usual factor 31/2 only for isotropic velocity distributions. Many people have been waiting for HST to solve the matter; early on it delivered good evidence from stellar velocity dispersions in a handful of cases (i.e. the January 1997 STScI press release) and M87 did us a real favor by having a coherent rotating disk of gas. This problem became much more tractable with the simultaneous 2-dimensional coverage provided by STIS. There is now fair evidence (tracing back to Kormendy & Richstone 1995 ARA&A 33,581) that central pointlike masses occur as a constant fraction ~0.5% of the stellar mass in galaxies' spheroidal components, based on limited kinematic data (Magorian et al. 1998 AJ 115, 228, Ferrarese & Merritt 2000 ApJL 539, L9) and more extensive modelling of the cusps in starlight produced as stars crowd around the central mass (van der Marel 1999 AJ 117, 744). This is especially interesting because it implies that central black holes are a fixed byproduct of spheroid formation, rather than predating galaxies as appeared likely for a while.
Many stars in a nonaxisymmetric potential will follow box orbits, looking somewhat like Lissajous figures. About as many stars must be going one way as the other, to give a large σ but small rotational velocity; the small net excess gives the rotational or pattern speed, like the bar of an SB galaxy. Spiral bulges, in contrast, are largely supported by rotation. So why do they otherwise look so much like ellipticals?
Hot gas in ellipticals: hydrostatics. X-ray data have established the presence of substantial amounts of gas at ~107 K in ellipticals, as well as spread throughout clusters. The temperature derives from the kinetic energy of stars, from which much of the gas must have come by enrichment arguments). Under these conditions, the gas cools very slowly (except under the special conditions of a cooling flow) so it stays put for long times. This allows a hydrostatic trace of the mass distribution, since the observed gas distribution must be stationary in the galaxy potential.
In a spherical potential, the pressure P must balance overlying material:
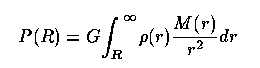
Some dwarfs may also have dark matter, based on radial-velocity dispersions of their brightest carbon stars (Aaronson 1983 ApJL 266, L11). Here progress is hard work - one must go star by star at very faint magnitudes. Since dwarfs are often found near massive galaxies (in part because we're sitting in one), tidal effects are important. Straightforward calculations suggest that many dwarfs will be quickly destroyed by their first close passage near a massive galaxy. More refined treatments show that they can cheat this estimate through
Central masses and elliptical dynamics: Simulations of the growth of massive black holes show that they will eventually alter the surrounding structure of the galaxy, removing stars on "death orbits" and making the central star distribution more spherical, thus cutting off their own source for mass growth (Merritt & Quinlan 1998 ApJ 498, 625). Strongly triaxial bulges (or bars) favor the population of chaotic orbits and thus growth of the central mass (Hasan & Norman 1990 ApJ 361, 69). Most conditions leave a "cusp" of stars with a roughly power-law radial distribution around the central mass (Quinlan, Hernquist, & Sigurdsson 1995 ApJ 440, 554), a result which dates back to less detailed calculations by Young in 1978. Such cusps are very common in both ellipticals and the bulges of early-type sprals.
Last changes: 9/2009 © 2000-2009